The net heat added to the gas must equal work done by the gas, by conservation of energy. The work done by the gas during the process A to B is
$\begin{align*}\int_A^B PdV = N k T\int_{V_1}^{V_2} dV/V = N k T \ln \left(V_2/V_1\right)\end{align*}$
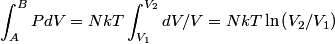The work done by the gas during the process B to C is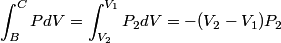
$\begin{align*}\int_B^C P dV = \int_{V_2}^{V_1} P_2 dV = - (V_2 - V_1) P_2\end{align*}$
There is no volume change in going from C to A, so no work is done by the gas. So, the net heat added to the gas is
$\begin{align*}N k T \ln \left(V_2/V_1\right) - (V_2 - V_1) P_2 = R T \ln \left(V_2/V_1\right) - R (T_h - T_c)\end{align*}$
Therefore, answer (E) is correct.

Solution to 1996 Problem 15